Some Figures From My PhD

art mathematics

Here is a small assortment of figures that I made during my PhD with the TWIST and INSPIRE groups, mainly for my thesis. I started to learn Blender shortly after the start of my PhD, but I ended up switching to POV-Ray, which is the tool used to create most of the images on this page (the only exception being the H-shaped skyrmion render, for which I used Blender). Although POV-Ray is significantly older and has fewer features than Blender, I have found it to be much more simple to use where more complex mathematics is required to describe an object (with Blender, I always felt like I was having to “hack” it in order to create what I wanted, even with the Python API).

The topology of a magnetic skyrmion comes from its homotopy group: the number of times the magnetisation covers a unit sphere is the skyrmion number \(N_{\mathrm{sk}}\). The texture defined over a unit sphere can be stereographically projected onto a two-dimensional plane.

This animation illustrates the principle of topological protection of skyrmions. For a skyrmion to be created by a continuous deformation of the topologically trivial collinear background, an antiskyrmion must be simultaneously created.

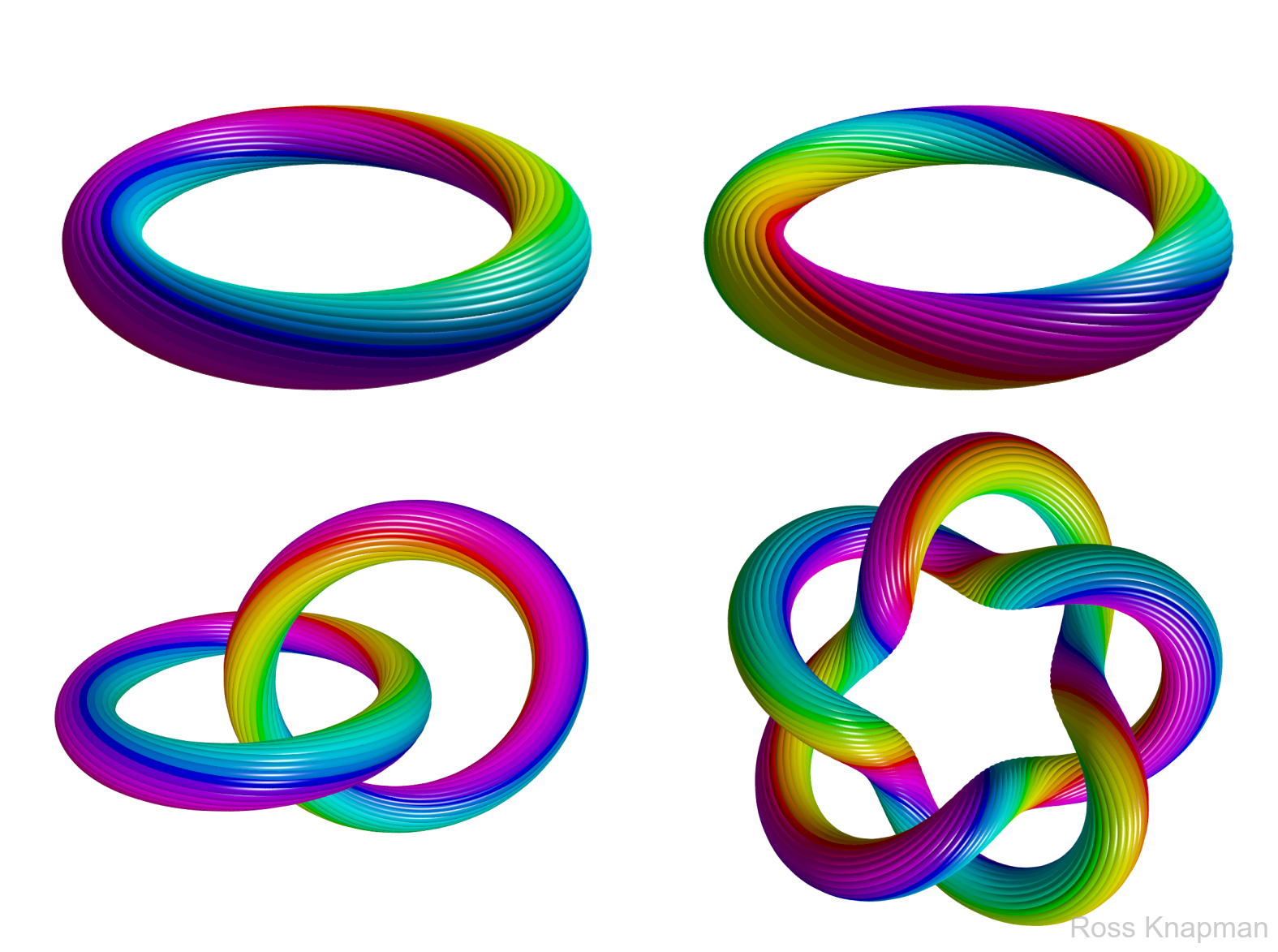
Hopfion of various orders.

Preimages of hopfions with various Hopf indices \(H\). \(H=1\) for a single twist, \(H=2\) for a double twist, \(H=4\) for two interlinked \(H=1\) hopfions, and \(H=8\) for a cinquefoil knot.

Magnetic hopfion constructed from skyrmions.

Magnetic hopfion texture from a tube of skyrmions.

Render of a H-shaped skyrmion.

A render of a H-shaped skyrmion. For more information on H-shaped skyrmions, see my publication on them.

Render the the Hopf fibration.

Hopf fibration visualised using a stereographic projection, which provides a way to view a 4D sphere in 3D! An explanation of the mathematics behind this is given by Niles Johnson on his website, which accompanies a beautiful video illustrating the Hopf fibration. He also has a lecture on the subject for real enthusiasts. Samuel J. Li also has an excellent interactive tool to demonstrate the Hopf fibration.